To get a taste of the issue, first consider the following abstract navigation problem -- hiking in foggy hills:
- There are only two useful landmarks, 1F (the origin or "first fix") and 2F (the destination or "second fix").
- It’s very foggy, so you have no way to use the hills as recognizable features. But the dead reckoning directions are of sufficient accuracy to get you within sight of landmark 2F. (For simplicity assume 100% accuracy).
- You don’t know and can’t measure hill slope angles. Indeed there are only two things the hikers can measure: (a) magnetic compass direction, and (b) distance actually walked. Observe that this is not distance as the crow flies, nor is it distance projected onto the horizontal plane. If a hill happens to be a pyramid, and you happen to be walking straight up it (and thus walking up the hypotenuse of a triangle), the distance measured is the length of the hypotenuse, not the length of the horizontal leg of that triangle.
- The first person who discovered 2F, starting from 1F, recorded dead reckoning directions to there and back as a sequence of tuples { direction, speed, time }.
Since we have insufficient information to determine "crow flight" distances, we don’t have enough information to accurately draw our dead reckoning itinerary on maps as we know them (i.e. Ptolemaic maps). Yet such faithfully recorded directions are sufficient to get any hiker (who can also exactly measure bearings and distances) from 1F to 2F and back.
Most maps as we know them – Ptolemaic maps -- are projections from a sphere to a Euclidean plane based on lines of latitude and longitude where lines of longitude converge at the celestial poles. Latitude is determined by measuring the altitude of a celestial object, and latitude is also ultimately defined by what navigators call the celestial sphere (although by "Ptolemaic map" I will refer to any map that shows actual earth surface distances proportionately on the map, i.e. "to scale"). There are also non-Ptolemaic maps, for example subway maps, which show the topological relationships between entities but not proportional distances. This chart of the kind Zheng He may have used, or was drawn using information from those or similar voyages, was of such a topological nature (the west coast of India is along the top and the east coast of Africa is along the bottom):

A subway map is in no way "to scale": the distances on are not proportional to any measured values. By contrast a dead reckoning map can be drawn "to scale" in its own distinct Euclidan plane. But not only cannot this dead reckoning space without further information be accurately projected (i.e. projected with proportions intact or "to scale") onto a Ptolemaic map, but two different dead reckoning itineraries drawn on a Euclidean plane will also generally be in error relative to each other, as I will describe below. And now to the central point I want to get across in this article: these two kinds of errors -- from trying to Ptolemaically map a dead reckoning itinerary on the one hand and between two dead reckoning itineraries on the other hand -- are very different. They are quite distinct in kind and usually produce errors of very different magnitudes.
The unknown values ignored in a dead reckoning itinerary, analogous to the hill slopes in the scenario above, can be any spatially variable but temporally constant distances, directions, or vectors that are unknown to the navigators writing and following the directions. The three most important spatially variable but temporally constant sets of vectors generally unknown to or ignored by dead reckoners on ocean and sea voyages from the 13th century through the era of the exploration explosion were were magnetic variation (shown below as green arrows), current (red arrows), and curvature of the earth (ignored in this post, but the same argument applies). Since these temporally constant but spatially variable factors (analogous to the slopes of our foggy hills) were unknown or ignored, they had no way to map such pure dead reckoning directions onto a Ptolemaic map. The information they rigorously measured and recorded for the purposes of dead reckoning was insufficient for that purpose. Yet that information was sufficient to enable navigators to retrace their steps (to get back on course if blown off course) or follow a previously recorded dead reckoning itinerary (or a nearby course, as I'll show below) with usefully small error.
Temporally constant but spatially variable vectors shown on a diagram. Only the dead reckoning (DR) vectors are shown added head-to-tail, since these are all the dead reckoning navigator in the exploration explosion era usually measured. The vectors shown here are magnetic variation (green) and current (red). Since these vectors were unknown, dead reckoning directions could not be accurately plotted on a Ptolemaic map. Curvature of the earth, not shown here, is also temporally constant and can thus also be ignored for the purposes of dead reckoning.
However some kinds of dead reckoning errors were due to unknowns variables that changed over time. These produced small but cumulative errors in dead reckoning even for the purposes of specifying repeatable directions. Errors in measuring bearing, speed, and time were of this nature. Externally, different winds required different tacking angles, creating "leeway", where the boat moves not straight forward but at an angle. If the directions don’t account for this, or account for it imperfectly, there will necessarily be a cumulative error. It was thus important to "fix" on landmarks or soundings. The more accuracy needed (such as when approaching shorelines, much more hazardous than open-ocean sailing), the more often fixes had to be taken. I hope to say more about fixes and temporally variable errors in future posts. This post is about dead reckoning between two fixes and errors that vary spatially but can be reasonably treated as constant in time.
A dead reckoning diagram made on a chart, with "fixes" or adjustments (dashed line)s to a landmark or sounding (yellow "X") diagrammed on the chart. The start and end of points of the voyage are also landmarks, so there is also a fix for the final landmark. Note that the chart still does not have to be Ptolemaic for this purpose -- the fixes need not be shown with proportionally correct distances to each other. Indeed the Zheng He era chart above is roughly in this form, with only one crude dead reckoning vector between each fix: it labels each arc with a crude time or distance estimate along with a (much more accurate) bearing estimate, but like a subway map it doesn't care about showing distances as proportional.
When sailing over continental shelves, European mariners (and sometimes Chinese mariners) of that era took "soundings" that measured depth and sampled the bottom soil, creating a unique signature of { depth, soil type} that functioned like landmarks but on open ocean. Soundings could be taken when sailing over the relatively shallow areas of continental shelves. As you can see, most parts of the oceans are too deep for this, but most shorelines are fronted by at least a few miles of soundable shelf, and sometimes hundreds of miles. Soundings were very useful for navigating in clouds, fog, and at night far enough away from the shore to avoid the hazards of very shallow water, yet close enough for the water to be shallow enough to sound. Pilots that used soundings thus had a set of "landmarks" for fixing their dead reckoning directions that allowed them to avoid hazardous navigation too close to land.
Notice that these kinds of fixes still do not give Ptolemaic coordinates -- they simply map or "fix" a particular point in our dead reckoning "space" to a particular point on the earth's surface of unknown Ptolemaic (celestial) coordinates, and indeed of unknown distances relative to other fixes.
(Side note -- explorers between Cao and Magellan usually could not get a celestial "fix" on a rolling deck of sufficient accuracy to be useful, i.e. more accurate than their dead reckoning -- and even in the case of Magellan this was only useful because there was nothing better, dead reckoning errors having accumulated to very high levels by the time they were in the mid-Pacific. So like them we will have to ignore this way, both more ancient and more modern, but generally unused during the exploration explosion, of correcting DR errors at sea).
It's all fine and good for dead reckoning to provide, as shown above, repeatable directions to a destination, despite being Ptolemaically unmappable, when the same itinerary is exactly repeated. But the best itinerary over the oceans depends on the wind. These winds vary, and the early explorers of new oceans searched for the best courses and seasons in order to catch the best winds. So the early explorers usually did not exactly repeat dead reckonings recorded on prior voyages. They usually took courses a few hundred miles away from the prior voyages' itinerary in order to catch more favorable winds. So the question arises: if the navigator adjusts his course by a few hundred miles, roughly what amount of resulting error should the navigator generally expect.
(BTW, it us important to note that dead reckoning directions, while they did not have to account for currents, magnetic variation, and the curvature of the earth, for the reasons given in this article, did have to account for variations in winds and the related leeway from tacking, since these reasons do not apply to vectors with substantial temporal variability. So we assume, as the navigators themselves probably did in some fashion, that the velocity vectors in our dead reckoning itineraries aren't strictly those measured, but are those measurements adjusted for variations in wind).
To reiterate the most important point: this is a different question than the question of what the error is when plotted on a normal map. Historians trying to recreate these voyages, in order to figure out where their landfalls were, or plot them on maps, or to estimate what navigational acccuracy of European navigators achieved in that era, usually haven't understood this crucial distinction. Indeed, because currents and magnetic variation don't in most places in the open ocean change in extreme or sudden ways, the resulting errors in dead reckoning navigation tended to be much smaller than the errors when plotting the dead reckoning directions on a Ptolemaic map. If you can scrutinize some more complicated diagrams I can demonstrate this by example here. First consider two dead reckoning itineraries, unadjusted for current and magnetic variation and thus plotted non-Ptolemaically:

Black = DR velocity in given time period
Red = average current velocity in given time period
Green = average magnetic variation in given time period
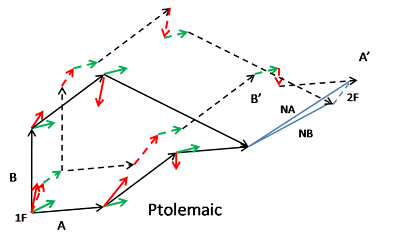
A, B = Two different DR itineraries as recorded (i.e. not adjusted for unknown magnetic variation and current). B has different first and third leg plus different currents on last two legs (only DR measurements added head-to-tail) – navigator would not actually plot these on a chart of geographic location, or at least would not consider such plotting accurate.
1F, 2F = first fix, next fix (same in each case, but their geographical location doesn’t need to be known)
For simplicity I am treating magnetic variation as uniform and spatially varying only the current, but the same argument I make here applies even more strongly to magnetic variation (and even more strongly to curvature of the earth, which can be treated as another set of vectors). The second fix (2F) has a question mark in front of it to indicate that the second itinerary (B) won't actually arrive at the same spot as A arrives at -- due to the different currents it encounters, it will arrive at a different spot. We assume, as was usually the case out of sight of shore, that our early explorer doesn't know the current. But the explorer did want to know, as historians want to know: roughly how large can such errors in typical oceans be expected to be? To demonstrate the mathematics of this, I've created a Ptolemaic map of the itineraries (dashed lines) by adding in the currents and magnetic variations head-to-tail. I've also superimposed the original non-Ptolemaic diagram (just the dead reckoning vectors added up) to show the much larger error that occurs when trying to project that onto a Ptolemaic map.
A‘, B’ = A and B adjusted to show difference in geographic location (all vectors added head-to-tail). The navigator in Columbus’ day could not usally compute these, since he typically did not know the current and magnetic variation values.
NA, NB = net effect of spatially variable but temporally constant current on geographic (i.e. Ptolemaic or celestial) location. Error if unadjusted itineraries Ptolemaically mapped. Separate red arrow diagram shows the same net effect of the two separate sets of currents.
Dashed blue line next to 2F = actual navigator’s error of two DR itineraries against each other when neither set of itineraries adjusts for current or magnetic variation. The next fix lies somewhere on this line, assuming no other errors.
(BTW if you can copy and paste arrows it's easy to make your own examples).
As you can see, the errors (solid blue lines labeled NA and NB) from trying to superimpose the non-Ptolemaic dead reckoning itineraries (solid lines) on the Ptolemaic map are much larger than the actual error (dashed blue line labeled 2F) that occurs from following itinerary A instead of B or vice versa (shown on dashed lines when adjusted for current. The magnetic variation is held constant, but the same argument applies to that, and to the curvature of the earth.
Note that the error in locating our second fix 2F is simply the same as the difference between the two separately added sets of current vectors:
It would be instructive to create a computer simulation of this which plugs in actual values (which we now know in excrutiating detail) for current, magnetic variation, and curvature of the earth.